Relasi

RELASI

• Relasi antara Ayah dan anak, Ibu dengan anak, dll
• Dalam aritmatika: Relasi besar atau kecil digunakan untuk membandingkan dua buah bilangan yang berdeda
• Binary Relation/Relation = relasi antara 2 objek

RELASI DALAM HIMPUNAN

• relasi dari himpunan A ke himunan B, artinya menetapkan setiap anggota pada himpunan        (x ∈  A) dengan anggota pada himpunan B (y ∈ B)
• relasi antara himpunan A dan himpunan B juga merupakan himpunan, yaitu himpunan yang pasangan berurutan yang mengikuti aturan tertentu, contoh (x,y) ∈ R
• Relasi biner R antara himpunan A dan B meruoakan himpunan bagian dari cartesian product A x B atau  R ⊆ (A × B)

             NOTASI DALAM RELASI

• Relasi antara dua buah objek dinyatakan dengan himpunan pasangan berurutan 
  (x,y) ∈ R
• contoh : relasi F adalah relasi ayah dengan anaknya, maka:
  F={9x,y) |x adalah ayah dari y}
• xRy dapat dibaca: x memiliki hubungan R dengan y
  contoh:
  Himpunan A : himpunan nama orang
  A={Via,Andre,Ita}
  Himpunan B : himpunan nama makanan
  B={es krim, coklat, permen}
  Relasi makanan kesukaan (R) dari himpunan A dan B adalah

CARA MENYATAKAN RELASI

• Diagram panah
• Himpunan pasangan berurutan
• Diagram Cartesius
• Tabel
• Matriks
• Graph Berarah

1. Diagram panah

      2.   Himpunan pasangan berurutan     

      3.   Diagram Cartesius

      4.  Tabel

     5.   Matriks

      6.    Graph Berarah

• hanya untuk merepresentasikan relasi pada satu himpunan (bukan antara dua himpuanan).
• Tiap unsur himpunan dinyatakan dengan sebuah titik (disebut juga simpul atau vertex).
• Tiap pasangan terurut dinyatakan dengan busur (arc).
• Jika (a, b) ∈ R, maka sebuah busur dibuat dari simpul a ke simpul b.
• Simpul a disebut simpul asal (initial vertex).
• simpul b disebut simpul tujuan (terminal vertex).
• Pasangan terurut (a, a) dinyatakan dengan busur dari simpul a ke simpul a sendiri. Busur semacam itu disebut loop

Contoh graph berarah
Misalkan R = {(a, b), (b, c), (b, d), (c, c) (c, a), (c, d), (d, b)} adalah relasi pada himpunan {a, b, c, d}.

 

SIFAT- SIFAT RELASI

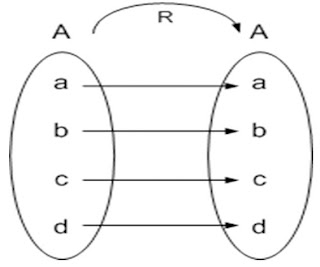
• Refleksif (reflexive)
• Transitif (transitive)
• SIMETRIK (SYMMETRIC)
• ASIMETRIK (ASYMMETRIC)
• ANTI SIMETRIK (ANTISYMMETRIC)
• EQUVALENT

1. Refleksif (reflexive)

Sebuah relasi dikatakan refleksif jika sedikitnya:

   x ∈ A,   xRx

Minimal

   2. Transitif (transitive)

• Sebuah relasi dikatakan bersifat transitif jika:
• xRy , yRz => xRz      ;         (x,y, z) ∈ A

Contoh:

  {R = {(a,d),(d,e),(a,e)}

   3.    SIMETRIK (SYMMETRIC)

• Sebuah relasi dikatakan bersifat simetris jika:
• xRy, berlaku pula yRx  untuk       (x dan y) ∈ A

Cotoh:

  A={a,b,c,d}

  R={(a,a),(b,b),(c,c),(d,d),(a,b),(b,a),(c,d),(d,c)}

  4.  ASIMETRIK (ASYMMETRIC)

• Relasi asimetrik adalah kebalikan dari relasi simetrik
• Artinya  (a,b) ∈ R, (b,a) ∉ R

Contohnya

R = {(a,b), (a,c), (c,d)}

 5.  ANTI SIMETRIK (ANTISYMMETRIC)

Relasi R dikatakan antisimetrik jika, untuk setiap x dan y di dalam A; jika xRy dan yRx maka x=y

6. EQUVALENT

• Sebuah relasi R dikatakan equivalen jika memenuhi syarat:

1. Refelksif
2. Simeteris
3. Transitif

Oleh         : Aji Khoirul Anwar 

NIM          : A11.2011.06170

Kel            : 4310